I rented a bike to get around here in Cambridge. It’s not a great bike, but it works. For powering the bike’s lights, instead of using batteries that need to be replaced, it has a dynamo that gets its source of rotational power from a little cog that touches my rear wheel. Thus, the relationship between the amount of light I get and my speed is like this:

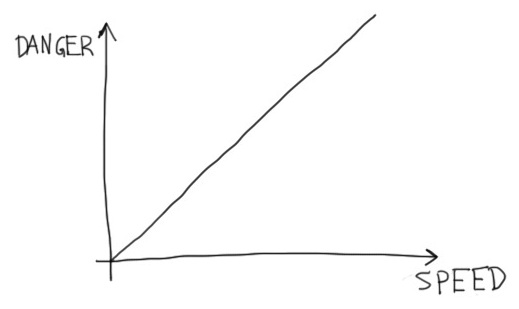
I only need the lights at night, on the back country roads near where I live (for the moment). It’s pretty dangerous on the back roads, what with potholes and gravel and hares running away from my hrududu. The relationship between how dangerous the biking is and how fast I am biking is like this:

Speed is the common variable in the first two graphs. Now, let’s look at the relationship between danger and light on the dark, back country roads:

Assuming that there is a certain level of light at which there is zero danger. But let us call our model a simplification for now.

The problem is that the independent variable, speed, is directly proportion to both danger and light. My goal when biking is to minimize danger. When there is not enough light, I have to speed up to get more. But then, I’ll end up going too fast and have to slow down, which immediately lessens my light, making it more likely that I will hit something, so I speed up again. All of this leads to the following:

So, I am, in essence, fucked when it comes to safety on the back country roads. There is an interesting degenerate case when I am at a full stop. There is no light, but I am in no danger because I am not moving. Unfortunately, my simplified model does not take into account other moving objects in the vicinity of the road.